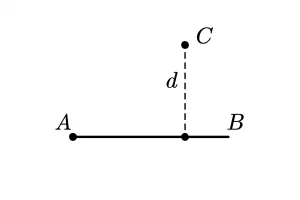
У нас есть окружность, заданная точкой её центра и радиусом. Еще у нас есть две точки, принадлежащие этой окружности — A и B, отсекая на окружности арку. Задача — построить между точками A и B еще n равноудаленных точек, принадлежащих окружности.
Если вам требуется сначала построить саму окружность (и вас есть три точки этой окружности), то воспользуйтесь вот этой статьей.
Задача не сложная — нам нужны углы точек A и B. Это углы, образованные точкой (A или B), центром окружности и осью X, проходящей через центр окружности. Их просто получить по следующим формулам:
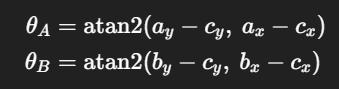
Далее мы получим разницу между этими углами дельта, которую надо будет поделить на равные N частей, чтобы построить равноудаленные точки на арке.
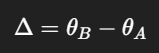
Точки по сути делят окружность на 2 дуги: короткую, либо длинную (более 180°). Я хочу, чтобы точки строилось по кратчайшей дуге, для этого я проверяю:
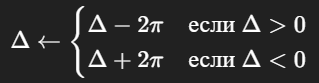
Далее вычислим шаг, поделив дугу на n + 1 частей:
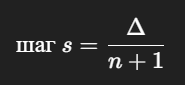
Углы искомых точек:
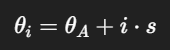
И их координаты:
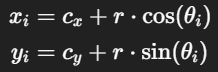
Реализация на JS
Осталось запрограммировать алгоритм на чем то простом. Для меня — это JS.
Входных параметров много, но ничего лишнего: cx, cy и r — описывают окружность, ax, ay, bx, by — точки A и B, ну и n — требуемое количество точек на арке.
Функция возвращает массив объектов с координатами: [{x1, y1}, {x2, y2} … {xn, yn}]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
// интерполяция заданного числа точек на арке окружности function interpolatePointsOnArc(cx, cy, r, ax, ay, bx, by, n) { let angleA = Math.atan2(ay - cy, ax - cx); let angleB = Math.atan2(by - cy, bx - cx); // нормализуем углы в диапазон 0 .. 2 * PI // это избавляет от головной боли с отрицательными значениями atan2 if (angleA < 0) angleA += 2 * Math.PI; if (angleB < 0) angleB += 2 * Math.PI; let delta = angleB - angleA; // проверяем длинная/короткая дуга if (Math.abs(delta) > Math.PI) { delta = delta > 0 ? delta - 2 * Math.PI : 2 * Math.PI + delta; } let step = delta / (n + 1); // считаем точки const result = []; for (let i = 1; i <= n; i++) { const angle = angleA + step * i; const x = cx + r * Math.cos(angle); const y = cy + r * Math.sin(angle); result.push({ x, y }); } return result; } |