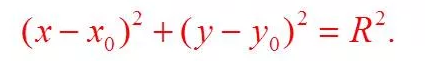
Координаты центра окружности по трем точкам

Обычно эта задача решается через уравнения круга, но для программирования нужно аналитическое решение (в виде формулы).

Если решать систему уравнений, пытаясь выразить все неизвестные величины через 6 координат известных точек, то можно получить выражения для Xo, Yo и R.

Но вид этих выражений и их последующая реализация в виде программного кода — мягко говоря — не вдохновляют начинать эту работу.

К счастью, есть алгебраический метод, сводящийся к ряду несложных поэтапных расчетов, которые позволяют вычислить искомые неизвестные.

Ниже прилагаю реализацию этого подхода в виде функции на javascript.

// на входе функция ожидает массив Z 
// с тремя точками-объектами вида {x: координата X, y: координата Y}
// на выходе получим X, Y, R - центр круга и его радиус
function getCircle(Z) {
  var A = Z[1].x - Z[0].x;
  var B = Z[1].y - Z[0].y;
  var C = Z[2].x - Z[0].x;
  var D = Z[2].y - Z[0].y;
  var E = A * (Z[0].x + Z[1].x) + B * (Z[0].y + Z[1].y);
  var F = C * (Z[0].x + Z[2].x) + D * (Z[0].y + Z[2].y);
  var G = 2 * (A * (Z[2].y - Z[1].y) - B * (Z[2].x - Z[1].x));
  if (G == 0) {
    // если точки лежат на одной линии, 
    // или их координаты совпадают,
    // то окружность вписать не получится
    return []; 
  }
  // координаты центра
  var Cx = (D * E - B * F) / G;
  var Cy = (A * F - C * E) / G;
  // радиус
  var R = Math.sqrt(Math.pow(Z[0].x - Cx, 2) + Math.pow(Z[0].y - Cy, 2));
  // вернем параметры круга
  return [Cx, Cy, R];
}

// на входе функция ожидает массив Z

// с тремя точками-объектами вида {x: координата X, y: координата Y}

// на выходе получим X, Y, R - центр круга и его радиус

function getCircle(Z) {

var A = Z[1].x - Z[0].x;

var B = Z[1].y - Z[0].y;

var C = Z[2].x - Z[0].x;

var D = Z[2].y - Z[0].y;

var E = A * (Z[0].x + Z[1].x) + B * (Z[0].y + Z[1].y);

var F = C * (Z[0].x + Z[2].x) + D * (Z[0].y + Z[2].y);

var G = 2 * (A * (Z[2].y - Z[1].y) - B * (Z[2].x - Z[1].x));

if (G == 0) {

// если точки лежат на одной линии,

// или их координаты совпадают,

// то окружность вписать не получится

return [];

}

// координаты центра

var Cx = (D * E - B * F) / G;

var Cy = (A * F - C * E) / G;

// радиус

var R = Math.sqrt(Math.pow(Z[0].x - Cx, 2) + Math.pow(Z[0].y - Cy, 2));

// вернем параметры круга

return [Cx, Cy, R];

}

Для тех, кому сложно читать код, и нужна чистая математика, привожу алгоритм рассчета:

Даны точки X(x1, y1), Y(x2, y3), Z(x3,y3), принадлежащие окружности с радиусом R и центром U(Cx, Cy).

A = x2 - x1;
B = y2 - y1;
C = x3 - x1;
D = y3 - y1;
E = A * (x1 + x2) + B * (y1 + y2);
F = C * (x1 + x3) + D * (y1 + y3);
G = 2 * (A * (y3 - y2) - B * (x3 - x2));
Если G = 0, это значит, что через данный набор точек провести окружность нельзя.
Cx = (D * E - B * F) / G;
Cy = (A * F - C * E) / G;

A = x2 - x1;

B = y2 - y1;

C = x3 - x1;

D = y3 - y1;

E = A * (x1 + x2) + B * (y1 + y2);

F = C * (x1 + x3) + D * (y1 + y3);

G = 2 * (A * (y3 - y2) - B * (x3 - x2));

Если G = 0, это значит, что через данный набор точек провести окружность нельзя.

Cx = (D * E - B * F) / G;

Cy = (A * F - C * E) / G;

Ну и останется найти радиус — как расстояние между одной из данных точек и найденным центром окружности.

Немного математики

Написать комментарий

Данная запись опубликована в 11.10.2019 02:36 и размещена в рубрике Программирование. Вы можете перейти в конец страницы и оставить ваш комментарий.

Мало букафф? Читайте есчо !

Тренажер для мозгов - перемножаем два числа в уме

Октябрь 18, 2012 г.

Для тренировки мышц нужны физические упражнения, а для тренировки мозга - умственные. Для тренировки мозга, в принципе, вообще ничего не надо, лишь найти место, где вас не будут отвлекать. Придумываем произвольную пару чисел, перемножаем. Берем следующую ...

Читать

Олимпиада для пятиклашек

Ноябрь 11, 2012 г.

Дочери (5й класс) на каникулы дали типа олимпиадки порешать. По математике. Ясно, что решают в итоге родители. Хорошо тем, кто в НИИ каком нить работает, или, может, профессорá, завалящиеся доценты с техническим уклоном имеются под рукой. А что делать ...

Читать

Комментарии к «Координаты центра окружности по трем точкам»

Понравилась статья? Есть вопросы? - пишите в комментариях.

Много комментариев в “Координаты центра окружности по трем точкам”

Юрий:

24 августа 2022 в 09:46

Алгебраический метод считает неправильно. Надо было посчитать: (-130;130)(200;200)(54.5;-336) дает неверный ответ (79,382;-54,014)

Ответить
- YURII:
  
  7 июля 2023 в 00:14
  
  Алгебраический метод считает правильно. Точки надо нумеровать в порядке возрастания по часовой стрелке.
  
  Ответить
  - YURII:
    
    7 июля 2023 в 20:14
    
    Алгебраический метод считает правильно независимо от порядка нумерования точек. Ищи ошибку у себя в расчетах.

Имя (обязательно)	Е-майл (не будет опубликован на сайте, обязательно для заполнения)
Комментарий: