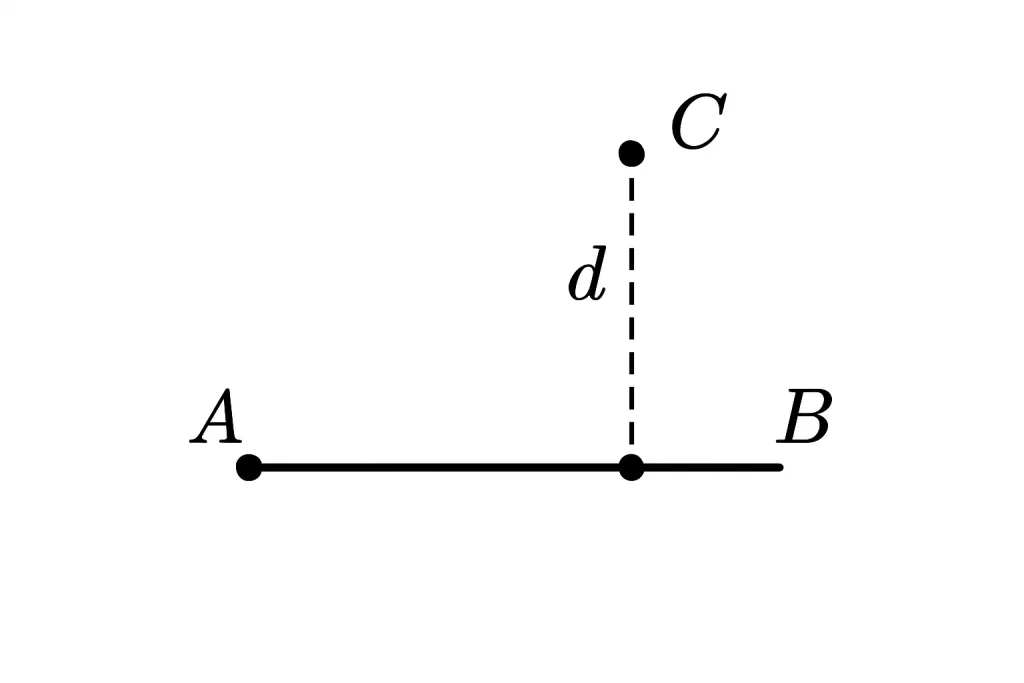
Методика заключается в поиске ближайшей точки на отрезке и зачем вычислении расстояния до этой точки.
Немного математики
У нас есть три точки — A, B и C. Мы хотим найти расстояние от точки C до отрезка AB. Т.е. расстояние от C до некоторой точки на отрезке AB. Эта точка не должна выходить за границы отрезка, как могло бы происходить в некоторых случаях, если бы мы искали расстояние от точки C до линии, проходящей через AB.
Найдем проекцию вектора AC на вектор AB:
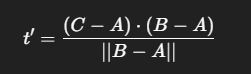
[A, B и C — это вектора из начала координат к соответствующим точкам.]
Если мы разделим это выражение еще раз на длину AB, то получим величину относительной проекции.
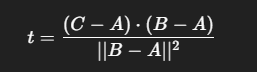
Которая позволит нам легко определить, чем является искомая ближайшая точка на отрезке AB:
- Если t < 0, ближайшая точка — это A
- Если t > 1, ближайшая точка — это B
- Если 0 ≤ t ≤ 1, ближайшая точка — внутренняя точка отрезка
Тогда ближайшую точку можно определить как:
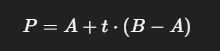
А расстояние:
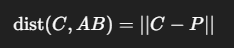
Код функции на JS
Теперь закодируем это в виде функции. Я использую JS, т.к. мне надо было решить эту задачу для JS. На входе — координаты всех трёх точек.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
function pointToSegmentDistance(ax, ay, bx, by, cx, cy) { const dx = bx - ax; const dy = by - ay; // квадрат длины AB const lengthSquared = dx*dx + dy*dy; // координаты точки P let px = ax; let py = ay; // отбросим кейс, если длина AB = 0 if (lengthSquared > 0) { // вычисление относительной проекции let t = ((cx - ax)*dx + (cy - ay)*dy) / lengthSquared; t = Math.max(0, Math.min(1, t)); // ограничиваем [0,1] // получим координаты P px = ax + t * dx; py = ay + t * dy; } // вычислим расстояние от C до P return Math.sqrt((cx - px)**2 + (cy - py)**2); } |

Результат первой формулы — это не «длина проекции», а сама проекция, т.е. скалярная величина, которая может быть отрицательной (в отличии от длины).
Благодарю за комментарий, Володя, поправил. Так действительно будет верно.