Очередная задача с литкода (№60. Permutation Sequence). В общем случае формулируется так: дан набор элементов, требуется вернуть этот набор после k перестановок.
О чем идет речь? Если у нас есть n элементов, то мы можем получить n! перестановок с их участием. Например у нас есть числа 1, 2, 3. Существует всего 6 перестановок: [[1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1]].
В задаче говориться о k-ой по счету перестановке, т.е. порядок получения этих перестановок тоже важен.
Как генерируются комбинации
Надо разобраться в технике того, как вообще генерируются комбинации. Используя рекурсию, можно написать следующий алгоритм:
Функция перебора:
- У нас есть массив элементов, мы перебираем их один за другим.
- Если массив пуст — выходим из функции
- Для каждого элемента делаем следующее — изымаем элемент из массива, и вызываем функцию рекурсивно (1). Возвращаем элемент в массив.
Если добавить передачу в функцию параметра, содержащего изъятые элементы, то мы при достижении дна массива (когда он на очередном рекурсивном витке станет пуст) можем сказать, что в функцию была передана очередная комбинация.
Если мы перебираем массив от начала к концу, это гарантирует нам особый порядок элементов, а именно в порядке возрастания комбинаций относительно порядкового номера элементов в массиве. Т.е. именно так, как в приведенном выше примере.
Огнем и мечом (грубой силой), O(N!)
Имея этот багаж знаний, можно уже решить задачу в лоб. Перебрать все комбинации, и вернуть ту, что требуется.
В задаче говорится, что у нас n может быть от 1 до 9, т.е. комбинаций всего 362880. Т.е., нет проблемы для получения результата даже грубой силой за отведенное время.
Конечно, я прибегну к некоторым трюкам, например, не буду тратить вычислительное время на модификацию массивов (изъятие элемента и вставку обратно).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
function getPermutation(n: number, k: number): string { // это наш пул значений, мы будем использовать // только n из них const pool = [1, 2, 3, 4, 5, 6, 7, 8, 9]; // счетчик кобминаций let count = 0; // функция возвращает накопленную комбинацию, // при этом триггером возврата является достижение // счетчиком требуемой комбинации k const perebor = (): string => { // хвост комбинации let res = ''; // также понадобится флаг // показывающий, что мы нашли в массиве // не использованный до сих пор элемент let flag = false; for (let i = 0; i < n; i ++) { const val = pool[i]; // чтобы не генерировать массивы // я прибегаю к маркировке использованных элементов if (val === 0) continue; flag = true; res = val.toString(); // элемент i использован - обнуляем его (маркируем) pool[i] = 0; res += perebor(); // восстановим элемент pool[i] = val; // если достигли k, // то пришло время собрать всю комбинацию: // вернем хвост выше по рекурсии if (count === k) return res; } // если все элементы были использованы // то мы достигли дна массива и // построили очередную комбинацию // проблема в том, что в данной ветке рекурсии // мы не видим всей комбинации, а только // знаем, что она собрана полностью. // т.е. функция годится только для поиска одной // комбинации. (но нас это устраивает) if (!flag) count ++; // вернем хвост комбинации return res; } return perebor(); }; |
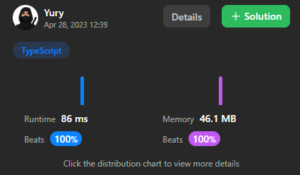
Это решение проходит критерии отбора на leetcode, конечно же с не самыми блестящими показателями.
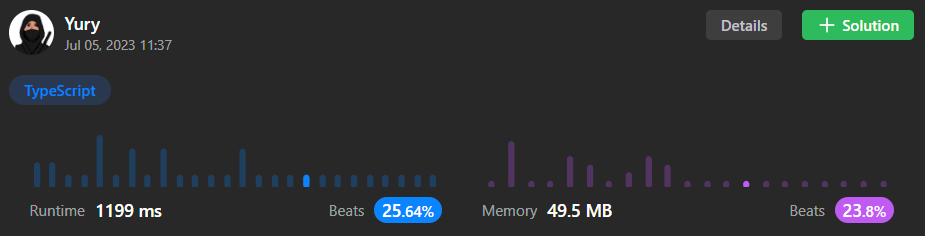
Алгоритм 2, с затратами O(N)
Понятно, что есть O(N) решение для этой задачи, где мы находим непосредственно элементы для каждой позиции i в диапазоне от [1 … n]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
function getPermutation_ON(n: number, k: number): string { const pool = [1, 2, 3, 4, 5, 6, 7, 8, 9]; let res = ''; for (let i = 0; i < n; i++) { // если взять общее число комбинаций // и прикинуть, где лежит наша требуемая k-я, // то мы сможем вычислить порядковый номер // элемента, который нужно использовать в k-й // комбинации. // например, n = 3, k = 6 - это явно где то в конце, // а точнее элемент '3'. const fact = factorial(n - i - 1); let fraction = Math.ceil(k / fact) res += pool[fraction - 1].toString(); // Раз уж мы использовали этот элемент, то уберем его из pool pool.splice(fraction - 1,1); // теперь надо понять дальнейшие шаги: // с выбором очередного элемента мы приближаемся к требуемому k // на кол-во позиций, которое будет зависеть от найденного элемента // возвращаясь к примеру: // если мы нашли '3', то мы тем самым должны 'пропустить' // 2! комбинаций * `позицию '3' в массиве, т.е. 2` = 4 k -= fact * (fraction - 1); // для следующего элемента это будет // 1! комбинаций * `позицию '2' в массиве, т.е. 1` = 1 } return res; }; function factorial(n: number): number { if (n <= 1) return 1; return n * factorial(n - 1); } |
Оптимизируем грубую силу
Забавно, но мы можем реализовать этот подход, обновив код первого алгоритма.
Если мы знаем, на какой итерации рекурсии мы находимся, то можно определить на сколько сильно влияет выбор очередного элемента. И если очередной элемент не позволяем нам достичь требуемого порядка k, то его можно пропустить.
Таким образом, рекурсия выродится до выбора правильной цифры и сведется, по сути, ко второму (быстрому) алгоритму.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
function getPermutation(n: number, k: number): string { const pool = [1, 2, 3, 4, 5, 6, 7, 8, 9]; let count = 0; const perebor = (depth: number): string => { if (depth === 0) { // на нулевой глубине // как и прежде увеличим счетчик // на единицу count ++; return '' } let res = ''; // цена шага на этой глубине рекурсии let nextStep = factorial(depth - 1) for (let i = 0; i < n; i ++) { const val = pool[i]; if (val === 0) continue; // если выбор элемента // не позволяет достичь k // при известной цене выбора // то пропустим элемент. if (count + nextStep < k) { count += nextStep; } else { res = val.toString(); pool[i] = 0; res += perebor(depth - 1); pool[i] = val; if (count === k) return res; } } return res; } return perebor(n); }; |
Вот, что удалось получить с модифицированным алгоритмом.
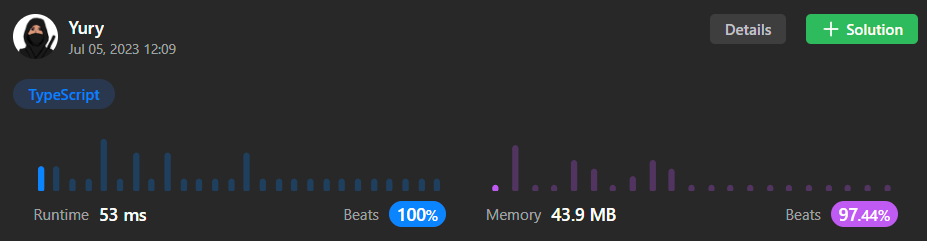
Он вроде бы не должен быть на столько быстрее, видимо, мне повезло получить немного больше вычислительных ресурсов, чем обычно. Во втором алгоритме, правда есть плохая функция Array.splice(), но мы же вызываем её всего N раз.