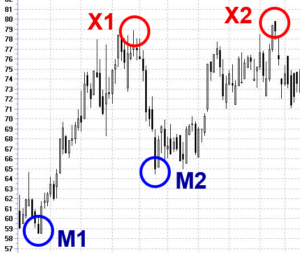
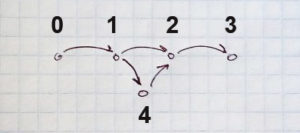
Задачу можно сформулировать так: представьте себе участок реки покрытый льдом и в первый день он полностью скован крепким льдом, позволяющим переправится по любому его участку. Разбив участок реки на R x C секторов, мы заявляем, что каждый день очередной сектор из сетки R x C становится не безопасным для пересечения. Нужно определить последний день, когда реку еще можно перейти по крепкому льду.
Да это, кстати, задача #1970 Last Day Where You Can Still Cross с литкода.
Строки (R) cекторов расположены вдоль русла реки, т.е. надо перебраться с r = 1 на r = R. В задаче даны R, С и массив опасных участков по дням [[ri, ci]], где i — это номер очередного дня.
Решение
Каждый день ситуация ухудшается и с определенного дня переправа становится не возможна. Понятно, что нам не нужно проверять каждый из дней, а можно использовать какой то поисковый алгоритм для определения конкретного дня. Например, бинарный поиск.
Т.е. алгоритм следующий — взяли день из середины текущего диапазона, проверили — можно ли пересечь реку в текущей ситуации. Если можно, то запомнили результат, и левую границу поискового окна сдвинули в середину. Иначе правую границу сдвинули в середину.
Проблема поиска пути
Граничные условия задачи предполагают, что R и C могут достигать 104. Это значит, что нужно как то оптимизировать поиск. Вместо поиска безопасного пути через реку, я буду смотреть нельзя ли прочертить путь вдоль реки по опасным участкам, т.к. именно они нам доступны как исходные данные. Если такой путь существует, то пересечь безопасно реку нельзя.
Давайте посмотрим детали реализации (TS).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
interface IState { r: number c: number } function latestDayToCross(row: number, col: number, cells: number[][]): number { const dir = [[0,1],[0,-1],[1,0],[1,1],[1,-1],[-1,0],[-1,1],[-1,-1]]; // ф-ция определяет можно ли пересечь реку // в n-ый день const canPass = (n: number): boolean => { // states - это текущие позиции, // что я отслеживаю, начинаю со столбца #1 (c == 1) const states: IState[] = [] // в pool храним оставшиеся доступные позиции. // я храню их там в упакованном виде: r + c * 10000 const pool: Set<number> = new Set(); for (let i = 0; i < n; i ++) { const [r, c] = cells[i]; // стартовые позиции. // вообще-то 'c' должно начинаться с нуля, // но автор задачи решил начать нумерацию с единицы. if (c == 1) states.push({ r, c }) // а прочие упаковываю в pool else pool.add(r + c * 10000); } while (true) { const state = states.pop(); // не удалось найти путь вдоль по // опасным участкам, значит существует // безопасный путь через реку if (state === undefined) return true const {r, c} = state // если нам удалось пересечь реку // по трещинам вдоль, то поперек // безопасного пути нет - вернем false if (c == col) return false // все возможные направления движения по трещинам // записаны в dir, переберём их for (const [dr, dc] of dir) { let nr = r + dr, nc = c + dc const key = nr + nc * 10000 if (pool.has(key)) { // следующий опасный участок добавляем в // массив перебора, при этом удаляем его из pool states.push({ r: nr, c: nc}) pool.delete(key) } } } } // бинарный поиск дня let L = 0, R = cells.length; let maxIndex = 0 while (L < R) { const mid = L + ((R - L) >>> 1); if (canPass(mid)) { L = mid + 1 if (maxIndex < mid) maxIndex = mid } else { R = mid } } return maxIndex }; |
Судя по статистике, это довольно эффективное решение (сравнивал среди JS решений), т.к. TS решений было недостаточно для показа графика.
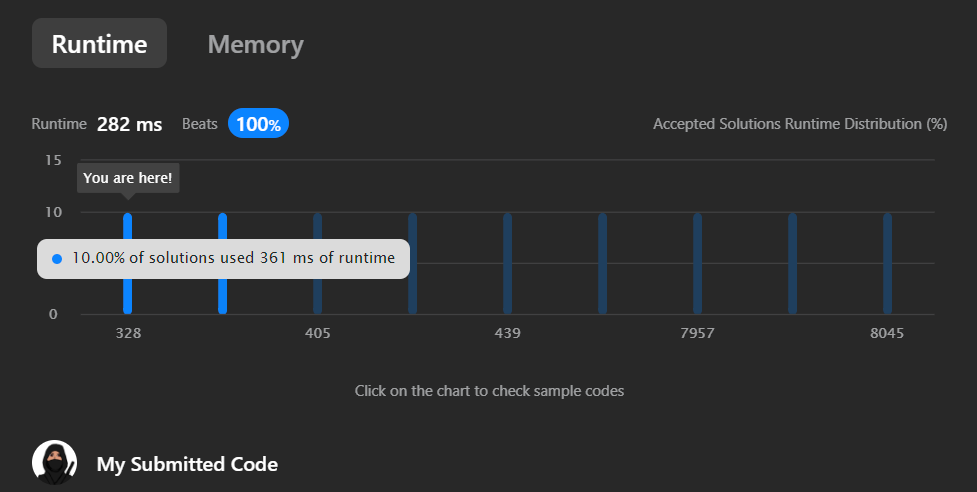
Сложнее всего, наверное, было психологически отказаться от традиционного использования массива-карты для поиска пути. Но вместо него пришлось использовать объект Set, т.к. нам нужно эффективно находить подходящие ячейки для следующего ходя, без перебора массива вручную.