Сегодня расскажу о решении задачи №1857 с литкода, которая называется как «Largest Color Value in a Directed Graph».
Суть задачи: дан направленный граф, при этом каждый узел имеет еще один параметр — его в задаче называют цвет. Спектр цветов ограничен, т.к. разные цвета обозначены в задаче разными латинскими буквами, т.е. максимальная палитра составляет всего 26 «цветов».
Требуется найти путь по графу, который собирает максимальное число узлов одного цвета. Дополнительно говорится, что если в графе есть петля, то нужно вернуть -1.
Подготовительные операции
Весь код далее написан на TS (typescript).
На входе мы получаем строку colors, которая задаёт цвет colors[i] для узла i. А также «ребра» направленного графа, массив элементов [j, k], который описывает переходы из узла j в узел k
|
1 |
largestPathValue(colors: string, edges: number[][]): number { ... } |
Почти всегда, когда граф задан подобным образом, приходится подготавливать данные, группируя информацию о переходах.
|
1 2 3 4 5 6 7 8 9 |
const dir: number[][] = new Array(colors.length); edges.forEach(elm => { const D = dir[elm[0]]; if (D === undefined) dir[elm[0]] = [elm[1]] else D.push(elm[1]); }) |
Это делается для того, чтобы не сканировать весь массива edges каждый раз, когда нам нужно будет установить куда можно перейти из текущего узла. Длина массива colors помогает определить число узлов.
Обход графа
Начальная идея очень проста — давайте начнем обход с узлов, у которых нет входящих переходов. Если таких узлов не обнаружится, то в графе имеются петли, мы вернем -1.
Процедура «обхода» будет использовать стек, который хранит историю пути и его статус. У нас получается такая структура:
|
1 2 3 4 5 6 |
interface IState { path: number[] // ноды в пути colCount: number[] // подсчет разных цветов - массив из 26 чисел colMax: number // максимум в массиве цветов pos: number // текущая нода } |
Для каждого узла со стека мы будет смотреть, куда нам можно из него перейти, и выполнять переход, обновляя статус.
Если перейти можно в узел, который уже есть в пути, то вернем -1 (петля).
Посмотрим реализацию идеи:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
interface IState { path: number[] colCount: number[] colMax: number pos: number } function largestPathValue_slow(colors: string, edges: number[][]): number { const dir: number[][] = new Array(colors.length); // этот массив послужит для определения: есть ли у узла входящие переходы. // изначально считаем что нет, и узел подходит для того, чтобы с него начать // обход (good for start) const starts: boolean[] = new Array(colors.length).fill(true) edges.forEach(elm => { const D = dir[elm[0]]; if (D === undefined) { dir[elm[0]] = [elm[1]] } else { D.push(elm[1]); } // в узел elm[1] есть переход // сбрасываем флаг starts[elm[1]] = false; }) // текущий макс для одного цвета let globeMax = -1 // перебираем все возможные старты for (let i = 0; i < starts.length; i ++) { if (!starts[i]) continue; // формируем начальное состояние стека const point = { path: [i], colCount: new Array(26).fill(0), pos: i, colMax: 1 } // индекс цвета вычисляем из ASCII кода символа point.colCount[colors.charCodeAt(i) - 97] = 1; const states: IState[] = [point] if (globeMax < 1) globeMax = 1 // обход узлов с помощью стека while (true) { const state = states.pop(); // пока стек что то содержит, выполняем обход узлов if (state === undefined) break; const D = dir[state.pos]; if (D !== undefined) { for (const elm of D) { // проверка не петля ли это if (state.path.includes(elm)) return -1 // состояние в новой точке графа const point = { path: [...state.path, elm], colCount: [...state.colCount], pos: elm, colMax: state.colMax } const colIndex = colors.charCodeAt(elm) - 97 point.colCount[colIndex] ++ // обновление максимумов if (point.colCount[colIndex] > point.colMax) { point.colMax = point.colCount[colIndex] if (point.colMax > globeMax) globeMax = point.colMax } states.push(point) } } } } return globeMax; }; |
Алгоритм работает, но довольно медленно для сложно разветвленных графов, т.к. то и дело проходит через одни и те же узлы. Фактически, это типичное слабое место рекурсивных алгоритмов.
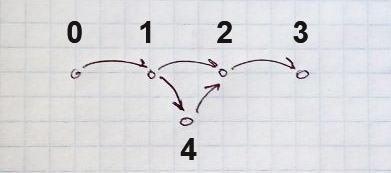
Любое разветвление заставит алгоритм пройти дважды оставшийся путь: — 0->1->2->3 или 0->1->4->2->3. Соответственно, если у нас есть 3 или более вариантов выхода из узла, то это служит как бы множителем числа вариантов обхода.
Топологическая сортировка
Чтобы не обходить узлы многократно, используем прием, который фактически является своего рода сортировкой узлов графа.
Мы уже начали прошлый алгоритм с того, что выделили узлы, в которые нет переходов из других узлов. А что если каждый раз искать подобные узлы, удаляя уже «отработанные переходы»?
На рисунке расписано 4 итерации такого «обхода».
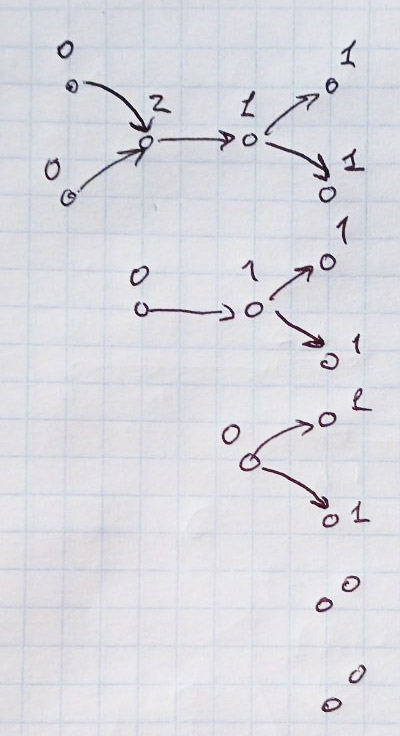
Над каждым узлом подписано число входящих переходов. Такой обход как бы «съедает» граф, удаляя отработанные узлы.
Отбор путей
Какую информацию нам нужно накапливать о состоянии обхода при переходе в очередной узел? Ответ на этот вопрос — основная сложность задачи.
Когда мы переходим в узел из пары других, то у нас как бы получается коллекция из двух состояний. Например, один родитель даёт цепочке цвет «a», а другой цвет «b». И далее цепочки должны это как то учитывать. Но нужно ли нам в данной задаче собирать коллекцию?
Т.к. речь идет о максимальном количестве узлов цвета в одном из путей, то достаточно собирать максимумы цветов.
Сбор коллекции состояний тоже будет работать, но гораздо медленнее и с большими затратами оперативной памяти.
Рассмотрим реализацию алгоритма.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
// структура для описания узлов interface INodeState { inputs: number // число входов colMax: number[] // максимумы цветов } function largestPathValue(colors: string, edges: number[][]): number { const dir: number[][] = new Array(colors.length); const starts: INodeState[] = new Array(colors.length) // инициализация описания узлов for (let i = 0; i < starts.length; i ++) starts[i] = {inputs: 0, colMax: new Array(26).fill(0) } // сбор первичной информации по узлам edges.forEach(elm => { const D = dir[elm[0]]; if (D === undefined) { dir[elm[0]] = [elm[1]] } else { D.push(elm[1]); } starts[elm[1]].inputs ++; }) let globeMax = -1 // чтобы ускорить поиск узлов, которые имеют 0 входов // на текущий момент, я использую стек const zeroInputsStack: number[] = []; // начальные узлы найдем "вручную" // а дальше будем пополнять стек во время обхода for (let i = 0; i < starts.length; i ++) if (starts[i].inputs == 0) zeroInputsStack.push(i) // обход while (true) { const i = zeroInputsStack.pop() // нет узлов - финиш if (i === undefined) break; const colIndex = colors.charCodeAt(i) - 97; if (!starts[i].colMax[colIndex]) { starts[i].colMax[colIndex] = 1; if (globeMax < 1) globeMax = 1 } // критерием петли у нас будет являться ситуация, // когда останутся не обработанные узлы // т.к. обработанные я маркирую -1 starts[i].inputs = -1 const D = dir[i]; if (D !== undefined) { D.forEach(N => { starts[N].inputs -- // пополнение стека новыми узлами if (starts[N].inputs == 0) zeroInputsStack.push(N) const colorIndex = colors.charCodeAt(N) - 97 // обновление максимума цветов // мы обновляем максимумы, добавляя цвет очередного узла for (let ci = 0; ci < starts[i].colMax.length; ci ++) { const addOn = (ci == colorIndex ? 1 : 0) if (starts[N].colMax[ci] < starts[i].colMax[ci] + addOn) { starts[N].colMax[ci] = starts[i].colMax[ci] + addOn; if (starts[N].colMax[ci] > globeMax) globeMax = starts[elm].colMax[ci] } } }) } } // проверка наличия петли for (let i = 0; i < starts.length; i ++) if (starts[i].inputs != -1) return -1; return globeMax; }; |