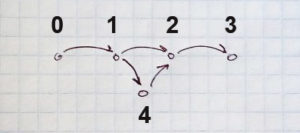
Решаем задачу с литкода о перетасовке строки.
Даны две строки, нужно определить является ли вторая строка результатом перетасовки букв в первой. Правила перетасовки следующие:
Мы произвольно делим строку на две подстроки, которые обозначим SX и SY. Далее мы можем переставить SX и SY местами, а можем не делать этого. Алгоритм может повторяться для SX и SY, до тех пор, пока строку можно еще разделить.
Например, для baloon и onloba — наша функция должна выдать true. Т.к. мы можем сначала поделить строку на ‘ba’ и ‘loon’, переставить их местами, а потом то же самое проделать с ‘loon’ — разделить на ‘lo’ и ‘on’ и тоже переставить местами.
|
1 2 3 4 5 |
[ba]-[loon] - разделили [loon]-[ba] - переставили [[lo]-[on]]-[ba] - разделили первую подстроку [[on]-[lo]]-[ba] - переставили части первой подстроки onloba - результат |
Другой пример — baloon и oblona — здесь функция должна выдать false, т.к. с помощью указанных выше правил перетасовки, мы не можем из 1й строки получить 2ю.
Решение
На leetcode в едитории подробно расписывается решение, основанное на методе динамического программирования. Это типичный подход для решения рекурсивных задач, но из-за многомерности пространства решения (число измерение больше 2) довольно сложно его понять, потому здесь я покажу решение с помощью рекурсии и мемоизации.
Рекурсия
Рекурсия следует прямо тем правилам, которые заданы задачей, их нужно только аккуратно запрограммировать.
Мы делим строку (изначально это S1) разными способами, и проверяем не является ли в свою очередь каждая подстрока результатом перетасовки. При этом мы проверяем два случая — с перестановкой частей строки и без этой операции. Нам нужно также знать позицию подстроки учитывая перестановки.
Когда длина подстроки будет равна 1, то нам нужно будет проверить не находится ли точно такой же символ на той же позиции в строке s2.
Звучит довольно просто, посмотрим код (typescript).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
function isScramble(s1: string, s2: string): boolean { // рекурсивная функция (s, pos) выполняет // проверку, можно ли из S получить подстроку в S2 в позиции pos, // пользуясь заданными правилами перестановки const check = (s: string, pos: number): boolean => { const n = s.length; // завершение рекурсии при длине == 1 if (n == 1) return s[0] == s2.charAt(pos) // перебираем варианты разделения строки for (let i = 1; i < n; i++) { // получаем подстроки const ns1 = s.substring(0, i), ns2 = s.substring(i) // проверяем без перестановки if (check(ns1, pos) && check(ns2, pos + i)) return true // проверяем с перестановкой if (check(ns1, pos + n - i) && check(ns2, pos)) return true } // если ни один из вариантов не подошел - то вернем false return false } return check(s1, 0) }; |
Код рабочий. Но понятно, что мы можем его оптимизировать.
Первое, что можно сделать, это отбросить проверки строк, которые точно не дадут положительного результата т.к. не содержат нужных символов.
Например, если вернуться к примеру с baloon и onloba , то мы можем разбить строку S1 на ‘bal’ и ‘oon’. Нет необходимости продолжать рекурсию для этих подстрок, так как очевидно, что подстроки S2 — ‘onl’, ‘oba’ не содержат тех же символов. И как бы мы не перетасовывали ‘bal’ , то не получим ‘onl’.
Это существенно ускоряет перебор, особенно для неглубокой перетасовки. Мы отсекаем ветки рекурсии с заведомо неправильным набором букв.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
function isScramble(s1: string, s2: string): boolean { const check = (s: string, pos: number): boolean => { const n = s.length; if (n == 1) return s[0] == s2.charAt(pos) // проверяем содержатся ли тот же набор букв // в строке s2, начиная с позиции pos const s1sort = s.split('').sort().join('') const s2sort = s2.substring(pos, pos + n).split('').sort().join(''); if (s1sort != s2sort) return false for (let i = 1; i < n; i++) { const ns1 = s.substring(0, i), ns2 = s.substring(i) if (check(ns1, pos) && check(ns2, pos + i)) return true if (check(ns1, pos + n - i) && check(ns2, pos)) return true } return false } return check(s1, 0) }; |
Для глубокой перетасовки этого мало, нужно как то оптимизировать ситуации, когда мы проверяем одинаковые подстроки, входя в разные ветки рекурсии. Например, разбивая baloon, мы получим подстроку ‘oon’ при разбиении [bal] — [oon] и при разбиении [ba]-[loon] -> [ba]-[[l]-[oon]].
Можно создать кеш, в котором мы будем, к примеру, запоминать результат проверки подстроки S в позиции POS, так мы отсечем уже ранее вычисленные результаты проверок.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
function isScramble(s1: string, s2: string): boolean { // получается, что нам нужен массив кешей // для каждой позиции POS свой собственный const cache: Map<string, boolean>[] = [] for (let i = 0; i < s1.length; i++) cache[i] = new Map(); const check = (s: string, pos: number): boolean => { const n = s.length; if (n == 1) return s[0] == s2.charAt(pos) const s1sort = s.split('').sort().join('') // как только мы получили сортированный набор // его можно тут же проверить в кеше const hist = cache[pos].get(s1sort) if (hist !== undefined) return hist const s2sort = s2.substring(pos, pos + n).split('').sort().join(''); if (s1sort != s2sort) { // кешируем результат cache[pos].set(s1sort, false) return false } for (let i = 1; i < n; i++) { const ns1 = s.substring(0, i), ns2 = s.substring(i) if (check(ns1, pos) && check(ns2, pos + i)) { // кешируем результат cache[pos].set(s1sort, true) return true } if (check(ns1, pos + n - i) && check(ns2, pos)) { // кешируем результат cache[pos].set(s1sort, true) return true } } // кешируем результат cache[pos].set(s1sort, false) return false } return check(s1, 0) }; |
Кеширование и использование встроенного объекта Map для организации кеша, позволяет существенно увеличить скорость перебора.
Алгоритм «не хватает звезд с неба», но даже по статистике leetcode выдаёт не плохие результаты.
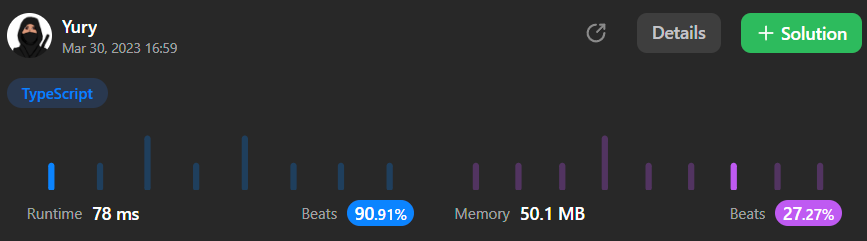
Видно, что кеш требует в среднем больше памяти, чем другие алгоритмы, но не плохо справляется с задачей в смысле быстродействия. Если потребуется, то мы можем пожертвовать частью быстродействия и сократить расходы памяти, для этого можно убрать одну или несколько точек кеширования (их 4 в коде).