Это еще одна классическая задача программирования о поиске некой лучшей пары чисел в массиве. Задача формулируется следующим образом.
Есть массив стоимости актива по дням, необходимо найти оптимальные точки покупки и продажи актива (входа и выхода из сделки). Обычно требуется найти максимальную величину прибыли в рамках периода, за который предоставлены данные.
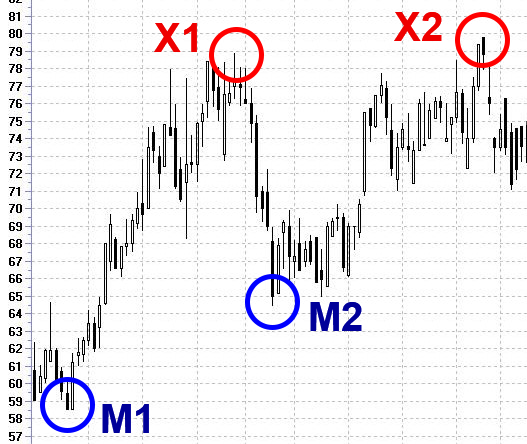
Рассмотрим произвольные данные биржевой динамики актива. Мне кажется, и без вычислений очевидно, где здесь точки входа и выхода. Это будут M1 и X2.
Brute force
Если решать эту задачу «грубой силой», нам нужно перебрать все элементы массива слева направо (i), и для каждого из них вычислять разницу с оставшимися элементами справа (j). Максимальная дельта и будет искомой величиной.
Ясно, что уже даже для массива в 10000 элементов, такие вычисления потребует времени, так мы перебираем элементы вложенными циклами. Число вычислений в цикле составит порядка N * N / 2.
Местные экстремумы
Совершенно ясно также, что для каждой точки массива, нас интересуют только самая минимальная величина актива слева от точки и максимальная величина справа от точки. И мы можем вычислить эти величины за один проход цикла.
Еще один проход цикла позволит найти максимум разницы между минимумами и максимумами в каждой точке. Т.е. число итераций циклов составит порядка 2 * N.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
function profit(prices: number[]): number { const min: number[] = []; const max: number[] = []; const len = prices.length; // находим минимумы и максимумы for (let i = 0; i < len; i ++) { let pr = prices[i]; min[i] = i === 0 ? pr : Math.min(min[i-1], pr); // максимум мы ищем на встречу минимумам, // потому индекс нужно предварительно вычислить const mxI = len - i - 1; pr = prices[mxI]; max[mxI] = mxI === len - 1 ? pr : Math.max(max[mxI + 1], pr); } // осталось найти максимальную дельту let bestDelta = 0; for (let i = 0; i < len; i ++) { const newDelta = max[i] - min[i]; if (newDelta > bestDelta) bestDelta = newDelta; } return bestDelta; }; |
Как видите, о затратах 2N можно говорить чисто формально, на деле это 3N, так как внутри первого цикла мы обращаемся к разным элементам массива. Хотя расчеты производятся существенно быстрее, но мы заплатили высокую цену в виде создания двух дополнительных массивов.
Поиск максимума
На самом деле мы делаем очень много лишних вещей, так как выполнить задачу можно с затратами порядка N и не создавая лишних массивов.
Двигаясь слева направо, нас интересует только самая минимальная точка слева. В то время как мы можем сравнивать её с каждым следующим значением и, таким образом, найти лучший результат за весь период всего за один проход цикла.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
function profit(prices: number[]): number { let min: number = 0; const len = prices.length; let res = 0; for (let i = 0; i < len; i ++) { let pr = prices[i]; // в min будем сохранять лучший минимум слева min = i === 0 ? pr : Math.min(min, pr); // каждый раз мы будем актуализировать // лучшую дельту const newDelta = pr - min; if (res < newDelta) res = newDelta } return res; }; |